发布时间:2026-01-30 14:52:46
编辑:Lisa来源:犀牛国际教育
AMC12竞赛考什么?AMC12数学竞赛考察的知识点包含了哪些?AMC12数学竞赛该怎么备考?AMC12数学竞赛的考察核心知识点包含哪些?考前如何复习?
AMC12 数学竞赛作为全球极具影响力的数学竞赛,涵盖高中数学核心知识与进阶拓展内容,题目兼具广度与深度。想要高效备考,精准把握AMC12考点、攻克重难点是关键!本文给大家汇总了这些要点,详情可接着往下看~
AMC12 必备知识图谱
一、代数模块(约40%)
◾多项式(因式分解、韦达定理、余数定理)
◾函数与方程(三角函数、指数对数函数、绝对值函数)
◾数列(等差等比通项与求和、递推数列)
◾不等式(均值不等式基础应用)
重难点:高次多项式因式分解、三角函数恒等变换、递推数列求解(易出错)
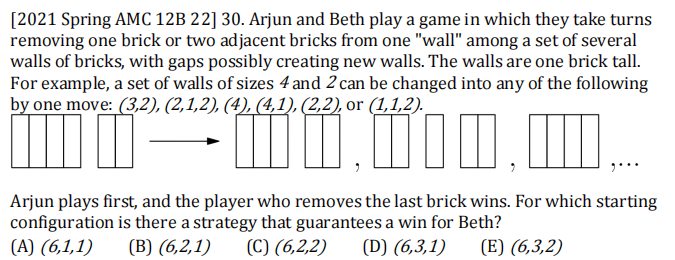
AMC12真题示例(代数)

二、几何模块(约25%)
◾平面几何(三角形全等相似、圆的基本性质与幂定理、不规则图形面积计算)
◾立体几何(常见立体图形表面积与体积、空间点线面位置关系)
◾解析几何(直线与圆的方程及位置关系)
重难点:圆的幂定理综合应用、立体几何截面问题(空间想象要求高)、直线与圆综合计算(计算量大需细心)。
AMC12真题示例(几何)
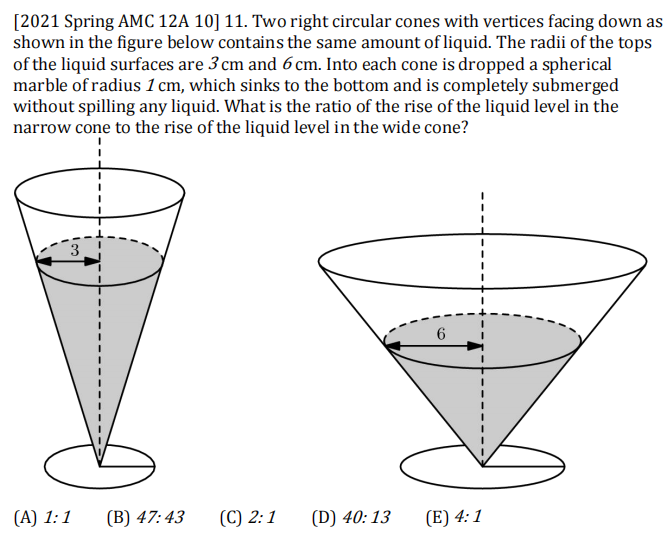
三、数论模块(约15%)
◾整数性质(整除、质合数判定、最大公约数与最小公倍数)
◾同余理论(模运算、费马小定理)
◾十进制与其他进制转换及运算
重难点:同余理论综合应用、质因数分解进阶技巧(解题关键)
AMC12真题示例(数论)

四、组合模块(约20%)
◾计数原理(加法与乘法原理、排列组合、容斥原理)
古典概型概率计算
◾组合构造与论证(抽屉原理)
重难点:限制条件下的排列组合(易遗漏重复)、抽屉原理构造性应用。
AMC12真题示例(组合)